You are using a web browser that is not fully supported by this website. Some features may not work as intended. For the best experience, please use one of the recommended browsers.

The Fundamentals of Biochemistry: Interactive Tutorials

10th Edition

A quantum mechanics study. Wingreen's paper is the first quantum mechanics calculation from first principles of two methane molecules in a box containing 63 or 139 waters. The two methanes do not stay apart. The equilibrium distance is 3.9 Å, which is the van der Waals contact distance, rCC, and the free energy is -15.8 kJ/mol relative to the hydrated monomers. However, the van der Waals interaction energy between two methane molecules is only -1.5 kJ/mol. So how does the system find the extra interaction energy to stabilize the dimer?

Figure 1: Hydration of Methane

A.) Displacement of water when two molecules of hydrated methane collide. r is the distance between carbon atoms.
B.) Number of waters within the first solvation shell of a methane pair. Dashed lines indicate a major plateau, between 4.4 and 5.4 Å, and two minor plateaus, between 5.4 and 5.8 Å, and between 6.0 and 6.5 Å.

Since a methane dimer is the most stable configuration, we have no direct information regarding the number of water molecules in the first hydration shell of the monomer. However, based on the methane clathrate model we can assume that the hydration number is about 24. Wingreen's results give 32 water molecules in the hydration shell of the dimer. Therefore the number of ordered water molecules in the system has decreased from 48 to 32. In other words, the hydrophobic effect has led to the release of 16 water molecules to bulk water.

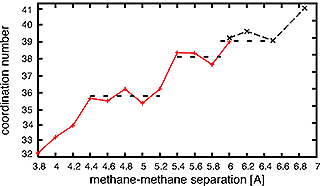
The two methane molecules within the solvent cage are not always in van der Waals contact with each other. Figure 1B shows the number of water molecules in the inner hydration shell as a function of the distance rCC. Besides a hydration number of 32 for lowest energy state, there are less stable states containing 36, 38, and 39 water molecules in the hydration shell (Fig. 1B). These numbers correspond to different sets of interlocked pentagons. Intermediate states, e.g. 37, have one or more hexagons, but as we saw from the methane clathrate model, water molecules forced into flat hexagons do not have ideal hydrogen bond geometry.

The key point is that water must be displaced from the hydration shells when two nonpolar molecules come together to form a complex.

2CH4·gH2O ⇌ (CH4)2·(g-i)H2O + iH2O

Water molecules lose entropy when they are forced into a hydration shell around nonpolar molecules. They gain entropy when they are free to return to the bulk solution, so that ΔS is positive. Therefore, -TΔS is negative. This favorable entropy change is an important contribution to the free energy change. Thus, Wingreen's results are in accordance with the traditional view of the hydrophobic effect.